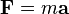Direct Current (red curve). The horizontal axis measures time; the vertical, current or voltage.

Direct current (DC) is the unidirectional flow of electric charge. Direct current is produced by such sources as batteries, thermocouples, solar cells, and commutator-type electric machines of the dynamo type. Direct current may flow in a conductor such as a wire, but can also flow through semiconductors, insulators, or even through a vacuum as in electron or ion beams. The electric charge flows in a constant direction, distinguishing it from alternating current (AC). A term formerly used for direct current was galvanic current.^[1]

Types of direct current.

Direct current may be obtained from an alternating current supply by use of a current-switching arrangement called a rectifier, which contains electronic elements (usually) or electromechanical elements (historically) that allow current to flow only in one direction. Direct current may be made into alternating current with an inverter or a motor-generator set.
The first commercial electric power transmission (developed by Thomas Edison in the late nineteenth century) used direct current. Because of the significant advantages of alternating current over direct current in transforming and transmission, electric power distribution is nearly all alternating current today. In the mid 1950s, HVDC transmission was developed, which is now replacing the older high voltage alternating current systems. For applications requiring direct current, such as third rail power systems, alternating current is distributed to a substation, which utilizes a rectifier to convert the power to direct current. See War of Currents.
Direct current is used to charge batteries, and in nearly all electronic systems, as the power supply. Very large quantities of direct-current power are used in production of aluminum and other electrochemical processes. Direct current is used for some railway propulsion, especially in urban areas. High-voltage direct current is used to transmit large amounts of power from remote generation sites or to interconnect alternating current power grids

Vectors

• Euclidean vector, a geometric entity endowed with both length and direction; an element of a Euclidean vector space. In physics, euclidean vectors are used to represent physical quantities which have both magnitude and direction, such as force, in contrast to scalar quantities, which have no direction.
  • Vector product, or cross product, an operation on two vectors in a three-dimensional Euclidean space, producing a third three-dimensional Euclidean vector
  • Vector projection, also known as the vector resolute, a mapping of one vector onto another
  • The vector part of a quaternion, a term used in 19th century mathematical literature on quaternions
  • Burgers vector, a vector that represents the magnitude and direction of the lattice distortion of dislocation in a crystal lattice
  • Displacement vector, a vector that specifies the change in position of a point relative to a previous position
  • Gradient vector, one vector in a vector field
  • Laplace–Runge–Lenz vector, a vector used chiefly to describe the shape and orientation of the orbit of one astronomical body around another
  • Normal vector, or surface normal, a vector which is perpendicular to a surface
  • Null vector, or zero vector, a vector whose components are all zero
  • Orbital state vectors, which define the state of an orbiting body
  • Position (vector), a vector which represents the position of an object in space in relation to an arbitrary reference point
  • Poynting vector, in physics, a vector representing the energy flux of an electromagnetic field
  • Tangent vector (disambiguation), a vector that follows the direction of a curve or a surface at a given point
  • Wave vector, a vector representation of a wave
• Gyrovector, a hyperbolic geometry version of a vector
• Axial vector, or pseudovector, a quantity that transforms like a vector under a proper rotation
• Basis vector, one of a set of vectors (a "basis") that, in linear combination, can represent every vector in a given vector space
• Coordinate vector, in linear algebra, an explicit representation of an element of any abstract vector space
• Darboux vector, the areal velocity vector of the Frenet frame of a space curve
• Four-vector, in the theory of relativity, a vector in a four-dimensional real vector space called Minkowski space
• Interval vector, in musical set theory, an array that expresses the intervallic content of a pitch-class set
• P-vector, the tensor obtained by taking linear combinations of the wedge product of p tangent vectors
• Probability vector, in statistics, a vector with non-negative entries that add up to one
• Row vector or column vector, a one-dimensional matrix often representing the solution of a system of linear equations
• Spin vector, or Spinor, is an element of a complex vector space introduced to expand the notion of spatial vector
• Tuple, an ordered list of numbers, sometimes used to represent a vector
• Unit vector, a vector in a normed vector space whose length is 1
• Vector, an element of a vector space

Realize you are responsible for your life. The decisions, the choices you make are yours. Don't blame others for things not working out, take responsibility, change the things that need changing.

join me ..............for more notes.................

A capacitor which is an energy-storage device is used to store energy between two conductors. These conductors are also called plates. An insulator is placed between these two plates. These plates are charged in order to store energy. One of the main function of a capacitor is to work as a filter. In this process blocks DC (Direct Current) and passes AC (Alternating Current).

There are various types of capacitors according to their designs and mechanisms. However, choosing a capacitor becomes quite interesting job, especially when we need to choose one according to our needs.

For Bypassing High Frequency to the Ground :

Ceramic Capacitor : It has relatively poorer capacitance. It is mostly used in a high frequency circuit. It looks like a disk in shape. It has dielectrics made of titanium acid barium. Basically, it is used to bypass high frequency to the ground.

Multilayer Ceramic Capacitor : Its function is same as a ceramic capacitor as it too is used to bypass signals of high frequency to the ground. It is a non-polarized capacitor ( So it comes in non polarized section too) . As per name, it contains a dielectric made of many layers of ceramic. It behaves well with extreme temperature and high frequencies.

For Large Value Capacitance :

Aluminum Capacitor : It consists of two electrodes. One being a negative and the other a positive one. Hence it has polarity. Largely, these electrodes are made of aluminum. The capacity of a electrolytic capacitor is measured on the scale of µF .The minimum capacity can be µF . While the maximum can lead to near 1000 µF. At some extent it shares its features with coils. Thus an electrolytic capacitor is not termed as something suitable for high-frequency circuits. Thus it is best used for low-frequency circuits where it works as a ripple filter.

Tantalum Capacitor : It is a type of electrolytic capacitor. The difference lies in the material used for the electrodes. As the name suggests, the electrodes for this type of capacitor is made of tantalum. However, in the matter of capacity it is better than any aluminum electrolyte capacitor. It is suitable for an analog circuit. Unlike an aluminum electrolytic capacitor, it is suits well for a high-frequency circuit. However, the making of a tantalum electrolytic capacitor needs more investment of money.

Super Capacitor : Termed by many as super capacitor only because its high level of capacitance. However, its actual name is electric double layer capacitor. It needs a lot of protective measures like a protection circuit to run it. Its high capacitance is prone to excessive inflow of electric waves which may be destructive to the circuit.

Non-polarized :

Mica Capacitors : This capacitor is one of the most expensive capacitors. However, it carries low capacitance. It is very safe for high voltage circuits, high frequency filters and resonance circuits. It, a non-polarized capacitor, comes with very high quality of insulation.

Polystyrene Film Capacitors : Basically, it is used as filter circuits. Like a multilayer ceramic capacitor, it too is a non-polarized capacitor. As the name says, polystyrene is used for the making of dielectric. Internally, it has a shape like a coil. Thus it can be found to be suitable for low-frequency circuits only.

• Physics Tutorial
  • 1-D Kinematics
  • Newton's Laws
  • Vectors - Motion and Forces in Two Dimensions
  • Momentum and Its Conservation
  • Work, Energy, and Power
  • Circular Motion and Satellite Motion
  • Thermal Physics
  • Static Electricity
  • Current Electricity
  • Waves
  • Sound Waves and Music
  • Light Waves and Color
  • Reflection and Ray Model of Light
  • Refraction and Ray Model of Light
• Minds on Physics
• The Calculator Pad
• Multimedia Studios
• Shockwave Studios
• The Review Session
• Physics Help
• Curriculum Corner
• The Laboratory
• The Photo Gallery

Vectors: Motion and Forces in Two Dimensions - Lesson 2

Projectile Motion

What is a Projectile? | Characteristics of a Projectile's Trajectory
Horizontal and Vertical Components of Velocity
Horizontal and Vertical Components of Displacement
Initial Velocity Components | Horizontally Launched Projectiles - Problem-Solving
Non-Horizontally Launched Projectiles - Problem-Solving

Student Extras

http://www.flickr.com/photos/physicsclassroom/galleries/72157625381723822/ Visit The Physics Classroom's Flickr Galleries and take a visual tour of projectile motion.
http://www.exploratorium.edu/skateboarding/trick02.html Learn about the physics of skateboarding.

Teacher's Guide

http://www.pbs.org/teachers/connect/resources/7897/preview/ View a lesson plan on the topic of projectile motion. The lesson plan centers around the physics of juggling and is presented by PBS Teachers.
http://www.physicsclassroom.com/shwave/projectile.cfm The Projectile Simulator activity from the Shockwave Studios is an excellent accompaniment for this reading.
http://www.physicsclassroom.com/curriculum/vectors/vect7.pdf This collection of sense-making activities from The Curriculum Corner will help your students understand projectile motion.
http://www.compadre.org/precollege/static/Unit.cfm?sb=2&Course=4&MID=8#Unit8 Need ideas? Need help? Explore The Physics Front's treasure box of catalogued resources on projectile motion.
Physclips: Projectiles View a collection of video clips and associated information related to projectile motion.
PhET Simulation: Projectile Motion This projectiles lesson from The Physics Classroom Tutorial provides a thorough background of projectiles to complement the PHET simulation.

What is a Projectile?

In Unit 1 of the Physics Classroom Tutorial, we learned a variety of means to describe the 1-dimensional motion of objects. In Unit 2 of the Physics Classroom Tutorial, we learned how Newton's laws help to explain the motion (and specifically, the changes in the state of motion) of objects that are either at rest or moving in 1-dimension. Now in this unit we will apply both kinematic principles and Newton's laws of motion to understand and explain the motion of objects moving in two dimensions. The most common example of an object that is moving in two dimensions is a projectile. Thus, Lesson 2 of this unit is devoted to understanding the motion of projectiles.
A projectile is an object upon which the only force acting is gravity. There are a variety of examples of projectiles. An object dropped from rest is a projectile (provided that the influence of air resistance is negligible). An object that is thrown vertically upward is also a projectile (provided that the influence of air resistance is negligible). And an object which is thrown upward at an angle to the horizontal is also a projectile (provided that the influence of air resistance is negligible). A projectile is any object that once projected or dropped continues in motion by its own inertia and is influenced only by the downward force of gravity.

By definition, a projectile has a single force that acts upon it - the force of gravity. If there were any other force acting upon an object, then that object would not be a projectile. Thus, the free-body diagram of a projectile would show a single force acting downwards and labeled force of gravity (or simply F_grav). Regardless of whether a projectile is moving downwards, upwards, upwards and rightwards, or downwards and leftwards, the free-body diagram of the projectile is still as depicted in the diagram at the right. By definition, a projectile is any object upon which the only force is gravity.

Projectile Motion and Inertia

Many students have difficulty with the concept that the only force acting upon an upward moving projectile is gravity. Their conception of motion prompts them to think that if an object is moving upward, then there must be an upward force. And if an object is moving upward and rightward, there must be both an upward and rightward force. Their belief is that forces cause motion; and if there is an upward motion then there must be an upward force. They reason, "How in the world can an object be moving upward if the only force acting upon it is gravity?" Such students do not believe in Newtonian physics (or at least do not believe strongly in Newtonian physics). Newton's laws suggest that forces are only required to cause an acceleration (not a motion). Recall from the Unit 2 that Newton's laws stood in direct opposition to the common misconception that a force is required to keep an object in motion. This idea is simply not true! A force is not required to keep an object in motion. A force is only required to maintain an acceleration. And in the case of a projectile that is moving upward, there is a downward force and a downward acceleration. That is, the object is moving upward and slowing down.
To further ponder this concept of the downward force and a downward acceleration for a projectile, consider a cannonball shot horizontally from a very high cliff at a high speed. And suppose for a moment that the gravity switch could be turned off such that the cannonball would travel in the absence of gravity? What would the motion of such a cannonball be like? How could its motion be described? According to Newton's first law of motion, such a cannonball would continue in motion in a straight line at constant speed. If not acted upon by an unbalanced force, "an object in motion will ...". This is Newton's law of inertia.


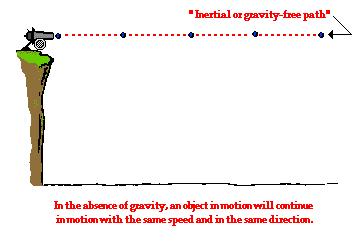
Now suppose that the gravity switch is turned on and that the cannonball is projected horizontally from the top of the same cliff. What effect will gravity have upon the motion of the cannonball? Will gravity affect the cannonball's horizontal motion? Will the cannonball travel a greater (or shorter) horizontal distance due to the influence of gravity? The answer to both of these questions is "No!" Gravity will act downwards upon the cannonball to affect its vertical motion. Gravity causes a vertical acceleration. The ball will drop vertically below its otherwise straight-line, inertial path. Gravity is the downward force upon a projectile that influences its vertical motion and causes the parabolic trajectory that is characteristic of projectiles.

 

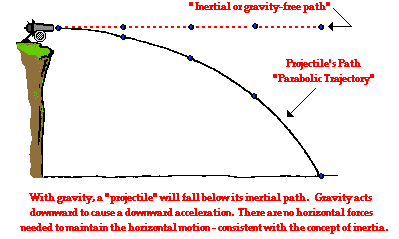
A projectile is an object upon which the only force is gravity. Gravity acts to influence the vertical motion of the projectile, thus causing a vertical acceleration. The horizontal motion of the projectile is the result of the tendency of any object in motion to remain in motion at constant velocity. Due to the absence of horizontal forces, a projectile remains in motion with a constant horizontal velocity. Horizontal forces are not required to keep a projectile moving horizontally. The only force acting upon a projectile is gravity!

Classical mechanics

Newton's Second Law

History of classical mechanics · Timeline of classical mechanics [show]Branches Statics · Dynamics / Kinetics · Kinematics · Applied mechanics · Celestial mechanics · Continuum mechanics · Statistical mechanics [hide]Formulations Newtonian mechanics (Vectorial mechanics) Analytical mechanics: Lagrangian mechanics Hamiltonian mechanics [show]Fundamental concepts Space · Time · Velocity · Speed · Mass · Acceleration · Gravity · Force · Impulse · Torque / Moment / Couple · Momentum · Angular momentum · Inertia · Moment of inertia · Reference frame · Energy · Kinetic energy · Potential energy · Mechanical work · Virtual work · D'Alembert's principle [show]Core topics Rigid body · Rigid body dynamics · Euler's equations (rigid body dynamics) · Motion · Newton's laws of motion · Newton's law of universal gravitation · Equations of motion · Inertial frame of reference · Non-inertial reference frame · Rotating reference frame · Fictitious force · Linear motion · Mechanics of planar particle motion · Displacement (vector) · Relative velocity · Friction · Simple harmonic motion · Harmonic oscillator · Vibration · Damping · Damping ratio · Rotational motion · Circular motion · Uniform circular motion · Non-uniform circular motion · Centripetal force · Centrifugal force · Centrifugal force (rotating reference frame) · Reactive centrifugal force · Coriolis force · Pendulum · Rotational speed · Angular acceleration · Angular velocity · Angular frequency · Angular displacement [show]Scientists Galileo Galilei · Isaac Newton · Jeremiah Horrocks · Leonhard Euler · Jean le Rond d'Alembert · Alexis Clairaut · Joseph Louis Lagrange · Pierre-Simon Laplace · William Rowan Hamilton · Siméon-Denis Poisson

v · d · e

Newton's First and Second laws, in Latin, from the original 1687 Principia Mathematica.

Prof. Walter Lewin explains Newton's first law and reference frames. (MIT Course 8.01)^[1]

Newton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces. They have been expressed in several different ways over nearly three centuries,^[2] and can be summarized as follows:

1. First law: Every body remains in a state of constant velocity unless acted upon by an external unbalanced force.^[3][4][5] This means that in the absence of a non-zero net force, the center of mass of a body either remains at rest, or moves at a constant velocity.
2. Second law: A body of mass m subject to a net force F undergoes an acceleration a that has the same direction as the force and a magnitude that is directly proportional to the force and inversely proportional to the mass, i.e., F = ma. Alternatively, the total force applied on a body is equal to the time derivative of linear momentum of the body.
3. Third law: The mutual forces of action and reaction between two bodies are equal, opposite and collinear. This means that whenever a first body exerts a force F on a second body, the second body exerts a force −F on the first body. F and −F are equal in magnitude and opposite in direction. This law is sometimes referred to as the action-reaction law, with F called the "action" and −F the "reaction". The action and the reaction are simultaneous.